 |
（３） 二等辺三角形の条件 (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
|
（３） 二等辺三角形の条件 (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
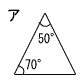
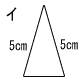
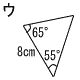
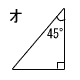
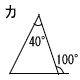
| １ | ア〜カの中から,二等辺三角形を3つ選んで,記号をかきなさい。 （ イ ） （ エ ） （ オ ） | ２ |  ２〜４について,空欄をうめて,証明を完成させなさい。 |
|||||||||||||||
 |
 |
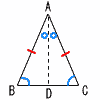 2つの角が等しい三角形は,二等辺三角形である（二等辺三角形の条件） ［証明］ 頂角Aの二等分線ADをひく △ABDと△ACDにおいて,
(1)(2)(4)より, 合同条件(１組の辺とその両端の角) がそれぞれ等しいから, △ABD≡△ACDで, AB＝AC |
||||||||||||||||
 |
 |
|||||||||||||||||
 |
 |
|||||||||||||||||
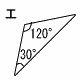| ３ | 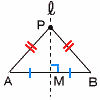 線分ABの垂直二等分線上に点Pをとるとき,PA＝PBとなる(線分の垂直二等分線の性質) ［証明］ △PAMと△PBMにおいて,
合同条件(2組の辺とその間の角) がそれぞれ等しいから, △PAM≡△PBMで, PA＝PB |
４ | 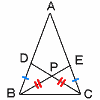 二等辺三角形の等辺に,BD＝CEとなる点D,Eをとるとき,△PBCは二等辺三角形となる［証明］ △EBCと△DCBにおいて,
がそれぞれ等しいから, △EBC≡△DCBで,∠EBC＝∠DCB 2つの角が等しいから, △PBCは二等辺三角形 |
|||||||||||||||
| ［トップに戻る］ ［問題に戻る］ |
［定義］
