 |
（２） 二等辺三角形の性質２ (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
|
（２） 二等辺三角形の性質２ (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
| １ | 二等辺三角形の頂角の二等分線を引くとき, 次の図の∠x の大きさを求めなさい。 |
 ２〜４について,空欄をうめて,証明を完成させなさい。 |
||||||||||||||||
| (1) | 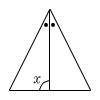 ∠x ＝90°（性質２） |
２ | 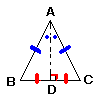 二等辺三角形の頂角の二等分線は,底辺を垂直に二等分する(二等辺三角形の性質) ［証明］ △ABDと△ACDにおいて,
合同条件(2組の辺とその間の角) がそれぞれ等しいから, △ABD≡△ACDで,BD＝CD さらに, ∠ADB＝∠ADC＝90° |
|||||||||||||||
| (2) | 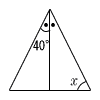 ∠x ＝180−(40＋90)＝50° |
|||||||||||||||||
| (3) | 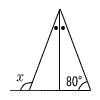 ∠x ＝180−80＝100° |
|||||||||||||||||
| ３ | 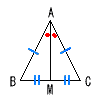 二等辺三角形の頂点Ａから底辺BCにひいた中線AMは,頂角を二等分する(二等辺三角形の性質) ［証明］ △ABMと△ACMにおいて,
合同条件( 3組の辺 ) がそれぞれ等しいから, △ABM≡△ACMで, ∠BAM＝∠CAM |
４ | 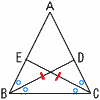 二等辺三角形の2つの底角の二等分線をBD,CEとするとき,BD＝CEとなる［証明］ △ABDと△ACEにおいて,
合同条件(1組の辺とその両端の角) がそれぞれ等しいから, △ABD≡△ACEで, BD＝CE |
|||||||||||||||
| ［トップに戻る］ ［問題に戻る］ |
［定義］
