（１３） 証明のしくみ ３ (解答) 学習日　 　 月　 　日（　　）
証明のステップ

　(1) 結論を含む合同な三角形を見つける
　(2) 仮定から合同条件をそろえる
　(3) 証明の形式通りに記述
正方形ABCDの対角線上にPがあるとき,
AP＝CPを証明しなさい。
　(ステップ１) 合同は,△PABと△PCB
　(ステップ２) 条件は,2辺とその間の角
　(ステップ３) 証明の形式にそって記述
　
空欄をうめて,次のことがらを証明しなさい。　
１ 　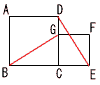2つの正方形ABCDとCEFGがあるとき,BG＝DEである。

［証明］

△BCGと △DCE において,

　 BC＝ DC　(正方形の１辺)
CG＝ CE　(正方形の１辺）
∠BCG＝ ∠DCE＝90°(内角)

合同条件(2辺とその間の角)
　　　がそれぞれ等しいから,

△BCG≡△DCEで, BG＝DE		 ２ 　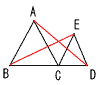2つの正三角形ABCとCDEがあるとき,BE＝ADである。

［証明］

△BCEと △ACD において,

　 BC＝ AC　(正三角形の１辺)
CE＝ CD　(正三角形の１辺)
∠BCE＝ ∠ACD＝120°(内角)

合同条件(2辺とその間の角)
　　　がそれぞれ等しいから,

△BCE≡△ACDで, BE＝AD
３ 　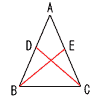二等辺三角形の等辺に,AD＝AEとなる2点をとると,BE＝CDである。

［証明］

△ABEと △ACD において,

　 AB＝ AC　（等　辺）
AE＝ AD　（仮　定）
∠BAE＝ ∠CAD（共　通）

合同条件(2辺とその間の角)
　　　がそれぞれ等しいから,

△ABE≡△ACDで ,BE＝CD		 ４ 　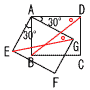長方形ABCDを30°回転して,長方形AEFGとすると,∠AGE＝∠ADBである。

［証明］

△AEGと △ABD において,

　 AE＝ AB　（短　辺）
AG＝ AD　（長　辺）
∠EAG＝ ∠BAD＝90°(内角)

合同条件(2辺とその間の角)
　　　がそれぞれ等しいから,

△AEG≡△ABDで,∠AGE＝∠ADB

［トップに戻る］ ［問題に戻る］