（１３） １次関数の利用３ (解答) 学習日　 　 月　 　日（　　）
移動の様子 → 時間と位置の関係をグラフに表す　
時速8kmの速さで,30分間走った。このとき,
　時間と進む距離の関係をグラフに表しなさい。
グラフ { 一定速度で動くとき…傾きのある直線
その場で停止(休憩)…x軸に平行な直線
　時速8kmで,30分間では4km
進むから,グラフは右図
　
２ 　800m離れた駅に行くのに,Ａさんは徒歩で,Ｂさんは自転車で行きました。右図は,8時x分に出発してym進んだ様子をグラフに表したものです。
(1) 　自転車のＢさんの分速を求めなさい。

　800mを4分で,800÷4＝200ｍ/分
　
(2) 　Ｂさんが駅に着いた時刻を求めなさい。

　グラフのアより, 8時12分
　		 (4) 　Ｂさんが駅に着いたとき,Ａさんは駅まであと何mの地点にいますか。

　グラフのイより, 200m
(3) 　Ａさんについて,yをx の式で表しなさい。

　800mを16分で,傾きは800÷16＝50
　　y＝50x		 (5) 　8時10分での,2人の距離の差を求めなさい。

　グラフのウより, 100m
　
　A町から12km離れたB町まで,120分間歩き,30分間休憩してから,30分走りました。x分後のスタート地点からの距離をykmとするとき,右図は様子をグラフに表したものです。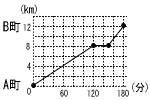
(1) 　歩いたとき,yをxの式で表しなさい。
　　　　（0≦x≦120）

　8kmを120分で,傾きは8÷120＝
　　y＝x
　　　		 (3) 　走ったとき,yをxの式で表しなさい。
　　　　（150≦x≦180）

　4kmを30分で,傾きは4÷30＝
　y＝x＋bに(180,12)を代入して,b＝−12
　　y＝x−12　
(2) 　休憩していたとき,yを式で表しなさい。
　　　　（120≦x≦150）

　距離yは変化せず一定で, y＝8
　　　		 (4) 　10km地点を通過したのは,スタートから何分後ですか。

　y＝x−12にy＝10を代入して,
　　10＝x−12より, y＝165分後　

［トップに戻る］ ［問題に戻る］