（１0） 連立方程式とグラフ(解答)	学習日　 　 月　 　日（　　）
連立方程式の解　⇔　方程式のグラフ(直線)の交点の座標 次の2直線の交点の座標を求めなさい。 　y＝2x＋1…ア 　y＝−x−2…イ 連立方程式の解を求めればよい。 ｛ y＝2x＋1…ア y＝−x−2…イ 　これを解いて,x＝−1,y＝−1 　　交点は （−1,−1）

　

次の連立方程式の解を,グラフをかいて求めなさい。
１	x＋y＝3…ア x−y＝1…イ アより,y＝−x＋3 イより,y＝x−1 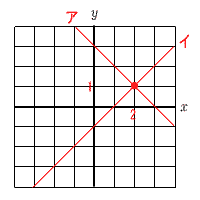グラフの 　交点は(2，1) 　x＝2，y＝1	２	3x＋y＝−2…ア x−y＝−2…イ アより,y＝−3x−2 イより,y＝x＋2 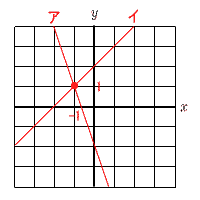グラフの 　交点は(−1，1) 　x＝−1，y＝1
次の直線アとイの交点の座標を,計算で求めなさい。
３	ア　y＝2x＋1 　イ　y＝−x＋4 連立方程式をつくると y＝2x＋1…ア y＝−x＋4…イ ア＝イより,2x＋1＝−x＋4 これを解いて,x＝1,y＝3 　　交点は　(1，3)	４	ア　y＝−3x−5 　イ　y＝2x＋5 連立方程式をつくると y＝−3x−5…ア y＝2x＋5 …イ ア＝イより,−3x−5＝2x＋5 これを解いて,x＝−2,y＝1 　　交点は　(−2，1)

［トップに戻る］ ［問題に戻る］