（８） １次関数の求め方 ２ (解答) 学習日　 　 月　 　日（　　）
2点から, 直線(1次関数)の式を求めよう
2点(3,7)と(5,11)を通る
　直線の式を求めなさい。

2点を通る直線は,連立方程式で		 （解）y＝ax＋bに,2点の座標を代入すると,
　 ｛ 　7＝3a＋b
11＝5a＋b
　　 これを解くと,a＝2,b＝1
　　　　　y＝2x＋1
　
直線の式を求めなさい。さらに,そのグラフもかきなさい。
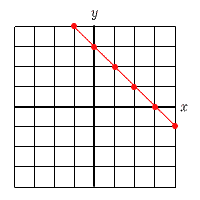
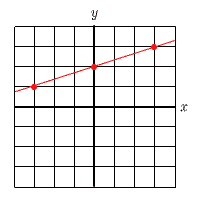
１ 　2点(1,2)と(2,1)を通る直線 ２ 　2点(−3,1)と(3,3)を通る直線
y＝ax＋bに2点の座標を代入すると,
2＝a＋b
1＝2a＋b
これを解いて,a＝−1,b＝3
　　y＝−x＋3		 y＝ax＋bに2点の座標を代入すると,
1＝−3a＋b
3＝3a＋b
これを解いて,a＝,b＝2
　　y＝x＋2
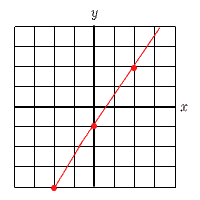
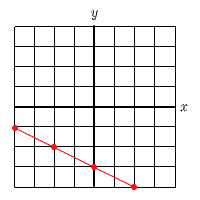
３ 　2点(−2,−4)と(2,2)を通る直線　 ４ 　切片が−3で,点(−4,−1)を通る直線　
y＝ax＋bに2点の座標を代入すると,
−4＝−2a＋b
　 2＝2a＋b
これを解いて,a＝,b＝−1
　　y＝x−1		 切片は−3だから,b＝−3

y＝ax−3に,x＝−4,y＝−１を代入して,
　−1＝−4a−3
　　4a＝−2より,a＝−
　 　y＝−x−3

［トップに戻る］ ［問題に戻る］