（２） 正多面体	学習日　　 月　 　日（　　）
正多面体は５種類あります。 　　（正４，６，８，１２，２０面体） 正多面体では， 　　１　どの面も,合同な正多角形 　　２　どの頂点にも,同じ数の面が集まる

印刷して、紙の上でやってネ！　　印刷用

１	正多面体は,次のように５種類あります。空欄をうめなさい。 名　　前 面　の　形 面の数 x 頂点の数 y 辺の数 z 見取り図 頂点に集まる面の数 x＋y−z 正四面体 　 　 ４ ４ 　 ３ ２ 正六面体 　 　 ６ 　 　 　 　 正八面体 　 　 　 ６ 　 　 　 正12面体 　 　 　 ２０ ３０ 　 　 正20面体 　 正三角形 　 　 ３０
２	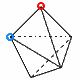右の図は, 2個の正四面体をくっつけたものです。 　この立体は「正多面体」といえるか, 空欄にあてはまる数やことばを入れて答えなさい。
	(1)	これは合同な正三角形が(　　　)個でつくられた多面体である。
	(2)	3つの正三角形が集まる頂点○は(　　　)個
	(3)	4つの正三角形が集まる頂点○は(　　　)個
	(4)	(1)(2)より, 各頂点に集まる図形の数が( 　　　　 )から,正多面体で( 　　　　 )