（１１） 円とおうぎ形１ (解答)	学習日　　 月　 　日（　　）
円（点Ｏは中心） 　半径OPが一定 おうぎ形（点Ｏは中心） 　弧と2つの半径で囲まれた図形

　

１	空欄に適する用語を入れなさい。		３	次の各図の∠x の大きさを求めなさい。
				(1)	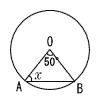半径OA＝OBで, 　△OABは二等辺三角形 2つの底角は等しいから, 　∠A＝∠Bで, 　∠x＝(180−50)÷2＝75°
	(1)	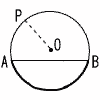右の円で, 　OPは（　半　径　） 　ABは（　　弦　　） 　は（　　弧　　）
	(2)	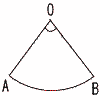右のおうぎ形で, 　OAは（　半　径　） 　OBは（　半　径　） 　∠AOBは（　中心角　） 　は（　　弧　　）		(2)	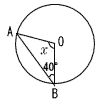半径OA＝OBで, 　△OABは二等辺三角形 2つの底角は等しいから, 　∠A＝∠B＝40°で, 　∠x＝180−40×2＝100°
２	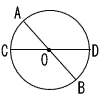次の図について,空欄に 　適する記号を入れなさい。 　　　（点Ｏは円の中心）			(3)	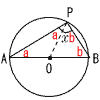ABが直径のとき, ∠xをOPで分けると, 　△OAPと△OBPは 　　　二等辺三角形だから, 　2∠a＋2∠b＝180° 　∠x＝∠a＋∠b＝90°
	(1)	AC＝（　BD　）
	(2)	∠AOC＝（∠BOD）		(4)	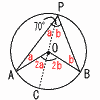∠APB＝70°のとき, ∠PをOPで分けると, 　∠P＝∠a＋∠b＝70° △OAPと△OBPは 　　　二等辺三角形だから, 　∠x＝∠AOC＋∠BOC 　　　＝2∠a＋2∠b＝70°×2＝140°
	(3)	＝（　　）