（３） 円と接線 (解答)	学習日　　 月　 　日（　　）
直線と円の位置関係は, 次の３通りある 　ア 離れている 　　　共有点なし 　イ 接している 　　　共有点1個 　　　（接点） 　ウ 交わっている 　　　共有点2個 　　　（交点）

　

１	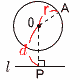円Ｏの半径をr ,円Ｏと直線l の距離をdとする。		３	次の各図で,∠xの大きさを求めなさい。 　　（Pは,直線 l と円Ｏの接点）
	(1)	d＞r のとき, 　直線と円の位置関係は 　　　（　離れている　） 　共有点の数は　0　個である。		(1)	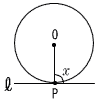∠x ＝90°
	(2)	d＜r のとき, 　直線と円の位置関係は 　　　（　交わっている　） 　共有点の数は　2　個である。		(2)	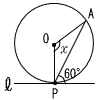90−60＝30° 　∠x ＝180−30×2 　　＝120°
	(3)	d＝r のとき, 　直線と円の位置関係は 　　（　接している　） 　共有点の数は　1　個である。		(3)	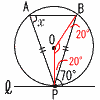△PABは二等辺三角形 　90−70＝20° 　180−20×2＝140° 　∠x ＝140÷2＝70°
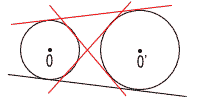
２	次の図のように,円Oと円O' の両方に接するような接線は,あと3本あります。下図にかき加えなさい。(正式な作図でなく,略図でよい)			(4)	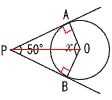点A,Bは接点 PとOを結ぶと, 　△OPAと△OPBは 　　直角三角形だから, 　∠x＝(90−25)×2 　　＝130°