|
(25) 滋賀県 | 学習日 月 日( ) |
|
(25) 滋賀県 | 学習日 月 日( ) |
~ 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)~
| 1 | ① .
③ 4b+3(2a-b) . ④ 8xy2×x÷(-2y)2 . ⑤ (2-√3)2+√12 . |
4 | ある中学校でバレーボール大会を行うことになった。どのチームも他のすべてのチームと1回ずつ対戦するとしたとき,チーム数ごとに総試合数はいくらになるかを求め,表にまとめることにした。
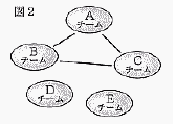 ① 3チームの場合,図2のようにA,B,Cのチームが3本の線で結べるので,総試合数は3試合であることがわかった。これを参考にして,5チームの場合の総試合数を求めなさい。 ① 3チームの場合,図2のようにA,B,Cのチームが3本の線で結べるので,総試合数は3試合であることがわかった。これを参考にして,5チームの場合の総試合数を求めなさい。. ② mチームの場合の総試合数をn試合としたとき,(m+1)チームの場合の総試合数を,mとnを用いた式で表しなさい。 . |
|||||||||||||||||||
| 2 | 次の連立方程式を解きなさい。
. |
5 | 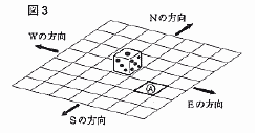 ① 操作<1>,<2>を2回繰り返したとき,さいころが,もとの中央の位置へもどる確率を求めなさい。 ① 操作<1>,<2>を2回繰り返したとき,さいころが,もとの中央の位置へもどる確率を求めなさい。. ② 操作<1>,<2>を3回繰り返したとき,さいころがAのマス目に移動したとする。このとき,さいころの上の目の数は何になるか。考えられる目の数をすべて書きなさい。 . 【操作】 <1> 4枚のカードをよくきって,その中から1枚を取り出す。 <2> 取り出したカードが示す方向にさいころを倒して隣のマス目に移す。 |
|||||||||||||||||||
| 3 | 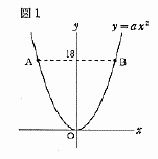 図1のように,関数 y=ax2 のグラフ上にy座標が18である2点A,Bがある。AB=6のとき,aの値を求めなさい。 図1のように,関数 y=ax2 のグラフ上にy座標が18である2点A,Bがある。AB=6のとき,aの値を求めなさい。. |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |