 |
（１０） 円と相似１（解答） | 学習日 月 日（ ） | ||||
|
||||||
|
（１０） 円と相似１（解答） | 学習日 月 日（ ） | ||||
|
||||||
 相似な三角形を記入して(対応をつけること),∠x,∠yの大きさ, 辺の長さxを求めなさい。 |
|||
| １ | 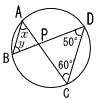 △PAB∽ △PDC ∠x＝50°(  の円周角)∠y＝60°(  の円周角) |
２ | 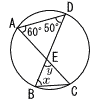 △ＡDＥ∽ △BCE ∠x＝60°(  の円周角)∠y＝180−(50＋60)＝70° |
| ３ | 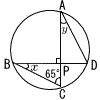 △PAD∽ △PBC ∠x＝90−65＝25° ∠y＝∠x＝25°( の円周角) |
４ | 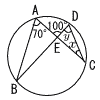 △ABE∽ △DCE ∠x＝100−70＝30° ∠y＝70°( の円周角) |
| ５ | 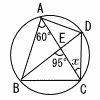 △ABE∽ △DCE △ADE∽ △BCE ∠x＝95−60＝35° |
６ | 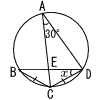 BC＝CDのとき,△ADE∽ △BCE △ACD∽ △DCE ∠x＝∠B＝30° |
| ７ | 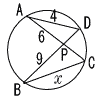 △PAD∽ △PBC x：4＝9：6 x＝4×9÷6＝6 |
８ | 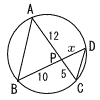 △PAB∽ △PDC x：12＝5：10 x＝12×5÷10＝6 |
| ９ | 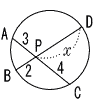 △PAB∽ △PDC△PAD∽ △PBC x：4＝3：2 x＝4×3÷2＝6 |
10 |  PA＝PCのとき,△PAB∽ △PDC PA＝PC＝yとすると, y：8＝2：yより,y＝4 5：x＝4：8 x＝5×8÷4＝10 |
| ［トップに戻る］ ［問題に戻る］ |
円の中の線分AC,BDに対して
