 |
（６） いろいろな円周角 (解答) | 学習日 月 日（ ） | ||||||||
|
||||||||||
|
（６） いろいろな円周角 (解答) | 学習日 月 日（ ） | ||||||||
|
||||||||||
 次の図で，∠x,∠y の大きさを求めなさい。(点Oは円の中心) |
|||
| １ | 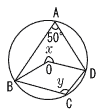 ∠BOD＝50×2＝100° ∠x＝360−100＝260° 中心角の半分 ∠y＝260÷2＝130° |
２ | 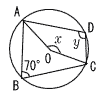 円周角の2倍 ∠x＝70×2＝140° 中心角の半分 ∠y＝(360−140)÷2＝110° |
| ３ | 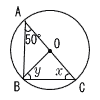 ∠ABC＝90° ∠x＝180−90−50＝40° OA＝OB(半径)より ∠y＝∠x＝40° |
４ | 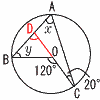 中心角の半分 ∠x＝120÷2＝60° ∠BDO＝＝60＋20＝80° ∠y＝120−80＝40° |
| ５ | 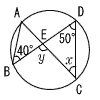 同じ弧に対する円周角 ∠x＝∠B＝40° ∠Eの外角 ∠y＝∠C＋∠D＝40＋50＝90° |
６ | 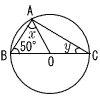 OA＝OB(半径) ∠x＝∠B＝50° ∠BAC(半円の円周角)＝90° ∠y＝180−90−50＝40° |
| ７ | 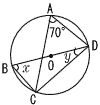 同じ弧に対する円周角 ∠x＝∠A＝70° ∠BCD(半円の円周角)＝90° ∠y＝180−70−90＝20° |
８ | 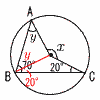 円周角の2倍 ∠x＝70×2＝140° ＯＡ＝OB＝OC(半径) ∠y＝70−20＝50° |
| ９ | 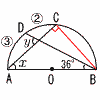  ＝3:2のとき∠CBD:36＝2:3で,∠CDB＝24° ∠x＝90−(24＋36)＝30° ∠y＝30＋36＝66° |
10 | 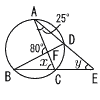 ∠B＝25° ∠x＝80−25＝55° △ACEで ∠y＝∠x−25＝55−25＝30° |
| ［トップに戻る］ ［問題に戻る］ |
円周角は
