（２）相似比 (解答)	学習日　 　 月　 　日（　　）
相似比とは, 対応する線分の長さの比 右の長方形で 　縦の長さ 4： 8＝1：2 }相似比 　横の長さ 6：12＝1：2 縦・横以外の 　対角線も1：2になっている

　

2つの図形は,それぞれ相似です。相似比とxの長さを求めなさい。
１	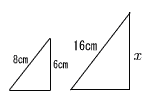相似比は　8:12＝2:3 　6:x＝8:12 　8x＝72より, x＝9	２	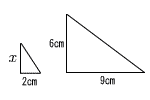相似比は　2:6＝1:3 　x:9＝2:6 　6x＝18より, x＝3
３	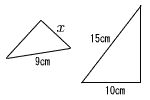相似比は　9:15＝3:5 　x:10＝9:15 　15x＝90より, x＝6	４	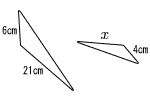相似比は　6:4＝3:2 　21:x＝6:4 　6x＝84より, x＝14
５	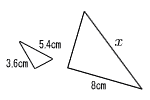相似比は　3.6:8＝9:20 　5.4:x＝3.6:8 　3.6x＝43.2より, x＝12	６	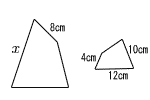相似比は 8:4＝2:1 　x:12＝8:4 　4x＝96より, x＝24
７	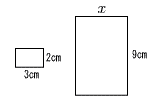相似比は 3:9＝1:3 　2:x＝3:9 　3x＝18より, x＝6	８	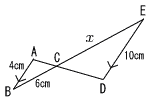△ABC∽△DEC 　相似比は　4:10＝2:5 　6:x＝4:10 　4x＝60より, x＝15
９	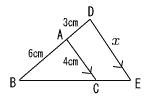△ABC∽△DBE 　相似比は 　　　　6:(6＋3)＝2:3 　4:x＝6:9 　6x＝36より, x＝6	10	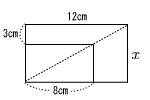外側は長方形 　相似比は　8:12＝2:3 　(x−3):x＝8:12 　12(x−3)＝8xより, x＝9
比例式 a：b＝c：d ⇒ ad＝bc (外項の積＝内項の積) x:3＝6:2　ならば　2x＝18で, x＝9

［トップに戻る］ ［問題に戻る］