（６） ２次関数と変域 (解答) 学習日　 　月　　 日（　　　）
変域とは, 変数x,yがとる｢値の範囲｣
y＝2x2（−2＜x ≦3）
　　　のグラフをかきなさい。
　また,このときのyの変域を求めなさい。
x,y の値を表にまとめると,　
x -2 -1 0 1 2 3
y 8 2 0 2 8 18
yの変域は,　0≦y≦18
　
１ 　y＝x2(−1≦x ≦2)のグラフをかきなさい。

　また,このときのyの変域も求めなさい。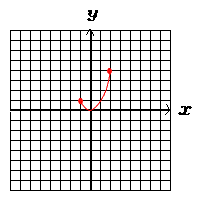













x＝−1のとき，y＝(−1)2＝1
x＝0のとき，y＝02＝0 (最小値)
x＝2のとき，y＝22＝4 (最大値)

　yの変域は, 0≦y≦4		 ２

　y＝−2x2(−2＜x≦１)のグラフをかきなさい。
　また,このときのyの変域も求めなさい。












x＝−2のとき，y＝−2×(−2)2＝−8
　　(最小に近い)
x＝0のとき，y＝02＝0 (最大値)
x＝1のとき，y＝−2×12＝−2

　yの変域は, −8＜y≦0　　
３

　関数y＝−x2において,xの変域が−1≦x≦2のとき,y の変域を求めなさい。


x＝−1のとき, y＝−(−1)2＝−1
x＝0のとき,　y＝02＝0 (最大値)
x＝2のとき, y＝−22＝−4(最小値)

　yの変域は, −4≦y≦0



　(注) 最大･最小値をグラフで確認！　　

 ４ 　2つの関数y＝ax2（aは定数）とy＝2x＋2は,x の変域が−1≦x≦3のとき,yの変域が同じになる。
　このとき,aの値を求めなさい。


y＝ax2の変域は，
　a＞0のとき, 0≦y≦9a …ア
　a＜0のとき, 9a≦y≦0 …イ

y＝2x＋2の変域は, 0≦y≦8 …ウ
　ウに合うのはアで, 9a＝8
　よって, a＝

［トップに戻る］ ［問題に戻る］