（５） 放物線の式 (解答)	学習日　 　月　　 日（　　　）
原点を通り, y軸対称な放物線の式は, y＝ax2 　 グラフが右の放物線になる 　　関数の式をかきなさい。 (2,8)を通るから, 　y＝ax2に,x＝2,y＝8を代入すると, 　　8＝a×22より,a＝2 　　　　(答）　y＝2x2

　

グラフが, 次のような放物線になる関数の式を求めなさい。
１	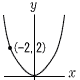y＝ax2に,x＝−2,y＝2を 　代入すると, 2＝a×(−2)2 　4a＝2 　a＝ 　　(答)　y＝x2	２	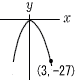y＝ax2に,x＝3,y＝−27を 　代入すると −27＝a×32 　9a＝−27 　a＝−3 　　(答)　y＝−3x2
３	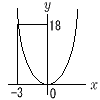y＝ax2に,x＝−3,y＝18を 　代入すると 18＝a×(−3)2 　9a＝18 　a＝2 　　(答)　y＝2x2	４	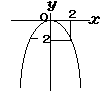y＝ax2に,x＝2,y＝−2を 　代入すると −2＝a×22 　4a＝−2 　a＝−1/2 　　(答) y＝−x2
５	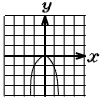y＝ax2に,x＝1,y＝−1を 　代入すると 　−1＝a×12 　a＝−１ 　　(答)　y＝−x2	６	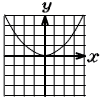y＝ax2に,x＝2,y＝1を 　代入すると 　1＝a×22 　4a＝1 　a＝ 　　(答)　y＝x2