 |
（７） さいころ (解答) | 学習日 月 日（ ） | |||
|
|||||
|
（７） さいころ (解答) | 学習日 月 日（ ） | |||
|
|||||
| １ |  大小2つのさいころを同時に投げるとき,次の確率を求めなさい。 |
２ |  さいころを続けて3回投げるとき,次の確率を求めなさい。 |
||
| (1) | 大が6,小が1の目が出る 目の出方は,全部で36通り 1÷36＝  |
(1) | 3回ともすべて,1の目が出る 1の目が1回は  ( )3＝1/216 |
||
| (2) | 2つとも同じ目が出る (大,小)＝(1,1)，(2,2)，…(6,6)の6通りで 6÷36＝  |
(2) | 3回ともすべて,同じ目が出る 同じ目は1〜6の6通り ( )3×6＝1/36 |
||
| (3) | 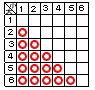 大の方が大きい目が出る対角線上を除く半分となる (36−6)÷2＝15通りで 15÷36＝  |
(3) | 3回ともすべて,偶数の目が出る 偶数の目が1回は  ( )3＝1/8 |
||
| (4) | 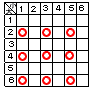 大が偶数,小が奇数の目右の表より9通りで 9÷36＝  |
(4) | 3回ともすべて,3以上の目が出る 3以上の目が1回は  ( )3＝8/27 |
||
| (5) | 少なくとも一方は偶数の目が出る (少なくとも一方は偶数) ＝(両方とも偶数)ではない 両方とも偶数は  だから,1−＝ |
(5) | 少なくとも1回は,偶数の目が出る (少なくとも1回は偶数) ＝(3回とも奇数)ではない 3回とも奇数は  だから,1−＝ |
||
| (6) | 大小の目の和が9となる (大,小)＝(3,6)，(4,5)，(5,4)，(6,3)で 4÷36＝  |
(6) | 3回の目の和が,4となる 1+1+2が3パターン ( )3×3＝1/72 |
||
| (7) | 大小の目の積が12となる (大,小)＝(2,6)，(3,4)，(4,3)，(6,2)で 4÷36＝ |
(7) | 3回の目の積が,奇数となる 3回とも奇数の目 ( )3＝1/8 |
||
さいころ2つを投げる場合