（４） いろいろな場合の数（解答）	学習日　 　 月　 　日（　　）
場合の数 並べかた(順　列) …順番に並べる場合 選びかた(組合せ) …順番を区別しない場合 場合の数とは,ことがらが 　何通り,何パターンあるかを数えたもの

　

次のような場合は,全部で何通りありますか。
１	(1)	3枚のカード を一列に並べる 方法(順列) 3×2×1＝ 6通り	２	(1)	3色の玉 から2つの玉を選ぶ 方法(組合せ) 　順番を区別しないから,2で割る 3×2÷2＝ 3通り
	(2)	4枚のカード を使って, 2桁の数を作る方法(順列) 　十位は0以外の3通り 3×3＝ 9通り		(2)	A,B,C,Dの生徒から,当番2人を 決める方法(組合せ) 　順番を区別しないから,2で割る 4×3÷2＝ 6通り
	(3)	リレーで,4人の選手A,B,C,Dが 走る順番(順列) 4×3×2×1＝ 24通り		(3)	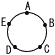円周上の5点A〜Eから,3点を 選んで三角形を作る方法(組合せ) 　順番を区別しないから,6で割る 5×4×3÷6＝ 10通り
３	(1)	AからBを通ってCへ行く道順 　　(ただし,途中で戻らない) 　A→Bは2通り　B→Cは3通り 2×3＝ 6通り	４	(1)	トーナメント戦を, 　　8チームで行う場合の試合数 　1試合ごとに,1チームが敗退 　　最終7チームが敗退で, 8−1＝ 7通り
	(2)	AからBへ行く道順 　　(ただし,途中で戻らない) 図のC,D,Eのいずれかを通る 　Cを通るコースは1　　Dを通るコースは4 　Eを通りコースは1 1＋4＋1＝ 6通り		(2)	リーグ戦を, 　　8チームで行う場合の試合数 　1チームにつき7試合で,8チーム 　　重複しているから, 7×8÷2＝ 28通り

［トップに戻る］ ［問題に戻る］