 |
（４） 多角形の外角の和 (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
|
（４） 多角形の外角の和 (解答) | 学習日 月 日（ ） | ||||||
|
||||||||
 次の図で,角度,またはxの値を求めなさい。 |
|||
| １ | 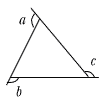 三角形の外角の和だから, ∠a＋∠b＋∠c＝360° |
２ | 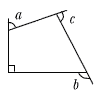 三角形の外角の和−90°で ∠a＋∠b＋∠c＝360−90＝270° |
| ３ | 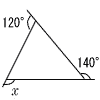 ∠x＝360−(120＋140)＝100° |
４ | 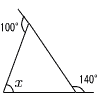 360−(100＋140)＝120 ∠x＝180−120＝60° |
| ５ | 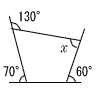 360−(130＋70＋60)＝100 ∠x＝180−100＝80° |
６ | 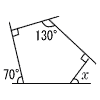 90＋70＋90＋50＝300 ∠x＝360−300＝60° |
| ７ | 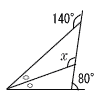 180−(360−140−80)＝40 ∠x＝140−40÷2＝120° |
８ | 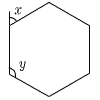 右の正六角形で∠x＝360÷6＝60° ∠y＝180−60＝120° |
| ９ | 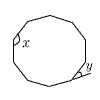 右の正十角形で∠x＝180−36＝144° ∠y＝360÷10＝36° |
10 | 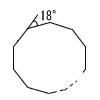 1つの外角が18°になる正多角形は,正x角形である。360÷18＝20 x＝20 |
| ［トップに戻る］ ［問題に戻る］ |
外角の和は,何角形でも360°→ n角形の外角の和は360°
五角形の外角の和を