（１２） １次関数の利用 ２ (解答) 学習日　 　 月　 　日（　　）
1次関数と図形(動点問題) → 点の動く距離と,三角形の面積との数量関係は,1次関数　　
点PがAからBまでxcm動くとき,
　△APDの面積をycm2とします。
　　yをxの式で表しなさい。
0≦x≦6で,
　　y＝×8×x＝4x

　　　y＝4x
　
１ 　AB＝6cm,BC＝4cm,∠B＝90°の直角三角形ABC上を点Pが,AからB,Cまで毎秒1cmの速さで進むとき,x秒後の△APCの面積をycm2とします。点Pが次の位置にあるとき,yをxの式で表しなさい。
(1) 　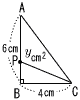点Pが辺AB上にあるとき,
　　　　（0≦x≦6）

　y＝×x×4
　y＝2x
 (3) 　(1),(2)のグラフをまとめてかきなさい。
(2) 　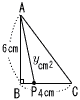点Pが辺BC上にあるとき,
　　　　（6≦x≦10）

　y＝×(10−x)×6
　y＝−3x＋30
２ 　１辺8cmの正方形の辺上を点Pが,AからB,C,Dまで毎秒2cmの速さで進むとき,x秒後の△APDの面積をycm2とします。点Pが次の位置にあるとき,yをxの式で表しなさい。
(1) 　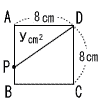点Pが辺AB上にあるとき,
　　　　（0≦x≦4）

　y＝×2x×8
　y＝8x
　　　		 (4) 　(1)〜(3)のグラフをまとめてかきなさい。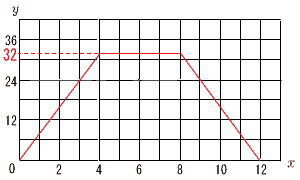
(2) 　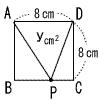点Pが辺BC上にあるとき,
　　　　（4≦x≦8）

　y＝×8×8
　y＝32
　　　
(3) 　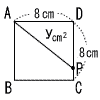点Pが辺CD上にあるとき,
　　　　（8≦x≦12）

　y＝×8×(24−2x)
　y＝−8x＋96

［トップに戻る］ ［問題に戻る］