（８）　分布と代表値２ (解答)	学習日　　 月　 　日（　　）
平均値（ミーン） 中央値（メジアン） 最頻値（モード） 範囲（レンジ） 　　中心傾向を示す 　　ゆがんだ分布に適する 　　流行とか人気 　　ばらつきを表す

　

１	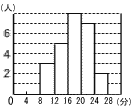右の図は,あるクラスで通学時間を調べて,ヒストグラムにまとめたものです。		２	次の表は,あるクラスの生徒が夏休み中に読んだ本の冊数をまとめたものです。 冊数 １ ２ ３ ４ ５ ６ ７ 計 人数 １ ３ ３ ６ ４ ２ １ 20
	(1)	度数分布表を完成しなさい。 階級(分) A 階級値(分) B 度数(人) A×B 以上 未満 　8〜12 10 3 30 12〜16 14 5 70 16〜20 18 8 144 20〜24 22 7 154 24〜28 26 2 52 　計 − 25 450		(1)	ヒストグラムをかきなさい。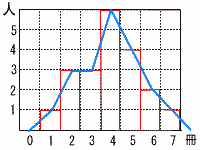
	(2)	(1)の表を使って,平均値を求めなさい。 　450÷25＝18分		(2)	(1)のヒストグラムをもとに,度数折れ線をかきなさい。 　（ヒストグラムに重ねてかき入れる） 　度数折れ線は,上の青線
	(3)	中央値（メジアン）を求めなさい。 25人だから,中央値は13人目 　16〜20分の階級値で, 18分		(3)	平均値を四捨五入で小数１位まで求めなさい。 (1×1+2×3+3×3+4×6+5×4+6×2+7×1) ÷20＝79÷20＝3.95で, 4.0冊
	(4)	最頻値（モード）を求めなさい。 人数の多いのは,8人の階級 　16〜20分の階級値で, 18分		(4)	中央値（メジアン）を求めなさい。 20人だから,中央値は10人目と11人目 　ともに4冊より,中央値は4冊
	(5)	範囲（レンジ）を求めなさい。 　26−10＝16分		(5)	最頻値（モード）を求めなさい。 　人数の多いのは6人で, 4冊