（５） 中央値　（解答） 学習日　　 月　 　日（　　）
中央値(ミーン) とは,中央に位置する値 → 大きさの順に並べたとき,真ん中にくる
　　　　　 ・7人(奇数)の得点の中央値
　　３ ４ ５ ６ ７ ９ １２　 (点)　→ 6点　
・ 8人(偶数)の得点の中央値
　３ ４ ５ ６ ７ ９ １２ 13　(点) → 8点　
　
１ 　それぞれのデータの中央値を求めなさい。 ２ 　表やグラフから中央値を求めなさい。
(1) 　5人の体重
　55, 48, 43, 44, 50　(kg)　
データを昇順に並び替えると,
　　43, 44, 48, 50, 55
3番目で,　中央値＝ 48kg		 (1) 　夏休み中に読んだ本の冊数
冊数 １ ２ ３ ４ ５ ６ ７ 計
人数 １ ３ ２ １ ５ １ ２ 15
累積 １ ４ ６ ７ 12 −
累積度数を調べて8番目で,中央値＝ 5冊
(2) 　8人のゲーム得点
　7, 6, 1, 9, 8, 5, 4, 2　(点)　
データを昇順に並び替えると,
　　1, 2, 4, 5, 6, 7, 8, 9
4.5番目で,　中央値＝(5＋6)÷2＝ 5.5点		 (2)
本数 １ ２ ３ ４ ５ 計
人数 １ ０ ２ ６ ５ 14
累積 １ １ ３ ９ −
生徒の筆記具の本数

度数分布表を作り,
7.5番目で,中央値＝ 4本
(3) 　6人の通学時間
　9, 7, 9, 16, 14, 11　(分)　
データを昇順に並び替えると,
　　7, 9, 9, 11, 14, 16
3.5番目で,　中央値＝(9＋11)÷2＝ 10点		 (3) 　今月の欠席者数
日数 ０ １ ２ ３ ４ ５ ６ 計
人数 17 ９ ６ ２ １ ０ １ 36
累積 17 26 −
累積度数をより,18.5番目で,中央値＝ 1日
３ 　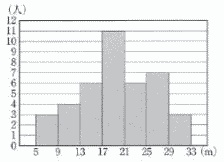40人のハンドボール投げの,ヒストグラムです。　
　度数分布表を完成し,中央値を含む階級を求めなさい。
 ４ 　中央値が7であるとき,xの値
　12, 5, 3, 9, 13, 6, 2, x　
データを昇順に並び替えて,
　2, 3, 5, 6, x, 9, 12, 13
4.5番目で,　中央値＝(6＋x)÷2＝7
　x＝14−6＝ 8　
階 級(m) 度数 累積度数
5以上〜9未満 3 3
9〜13 4 7
13〜17 6 13
17〜21 11 24
21〜25 6 30
25〜29 7 37
29〜33 3 40
　計 40 −
累積度数より,20.5番目で
　17ｍ以上21m未満


(注意)
　17〜21mの階級のどこに真の中央値があるのかはわからない。
　よって, 中央値≠階級値
　		 ５ 　平均値と中央値が同じとき,xの値
　1, 3, 5, x, 10, 12　
平均値＝(1＋3＋5＋x＋10＋12)÷6
　　＝(x＋31)÷6 …ア
中央値＝(5＋x)÷2 …イ
ア＝イより, x＋31 ＝ 5＋x
6 2
　　2(x＋31)＝6(5＋x)で, x＝8

［トップに戻る］ ［問題に戻る］