１年数学 　空間図形

こたえ 　〜　１年６章の正答　〜

１	ア	球	イ	円すい	ウ	円柱	エ	ドーナツ形
２	ア		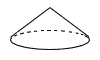イ	母線	ウ	円	４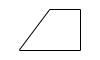
			エ	二等辺三角形	３	ひし形, 二等辺三角形

１	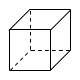立方体 　(正六面体)	２	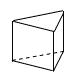正三角柱	３	円すい
４	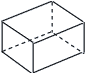直方体(四角柱)	５	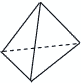正三角すい 　(正四面体)	６	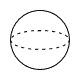球

１	ア	円柱	イ	正三角柱
	ウ	円すい	エ	立方体(正六面体)
	オ	正四角すい
２	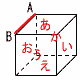組み立てると，左図のように 　面う は手前，面か は向こう側		ア	立方体(正六面体)
			イ	面い　，面え
			ウ	面う　，面か
	エ	面え	オ	面い　，面う　，面お　，面か

(９)　おうぎ形

１	l ＝2π×4×(90/360)＝2πcm Ｓ＝π×4２×(90/360)＝4πcm２	２	l ＝2π×6×(60/360)＝2πcm Ｓ＝π×6２×(60/360)＝6πcm２
３	l ＝2π×6×(240/360)＝8πcm Ｓ＝π×6２×(240/360)＝24πcm２	４	Ｓ＝×10×4＝20cm２
５	(1) 半径をrとすると， 　2πr＝2π×15×(120/360) 　2πr＝10π 　　r＝5cm	(2) 　底面積＝π×5２＝25π 　側面積＝15２π×(120/360)＝75π よって，表面積＝25π＋75π＝100πcm2

(10)　表面積

１	(4×4)×2＋(4×8)×4＝160cm２	２	(3×3)×6＝54cm２
３	(6×8÷2)×2＋(6＋8＋10)×6＝192cm２	４	22π×4＝16πcm２
５	(3×4÷2)×2＋(3＋4＋5)×4＝60cm２	６	42π＋8π×6÷2＝40πcm２
７	(42π÷2)×2＋8×(8π÷2)＋82＝(48π＋64)cm2	８	(5×8÷2)×4＋52＝105cm2

(11)　体　積

１	4×8×4＝128cm３	２	3３＝27cm３
３	6×8÷2×6＝144cm３	４	4２×6÷3＝32cm3
５	2２π×4＝16πcm３	６	6×6÷2×8÷3＝48cm3
７	4２π×6÷3＝32πcm３	８	42π÷2×8＝64πcm3

(12)　球

１	ア	Ｖ＝π×63＝288πcm3	２	ア	V=π×33＝36πcm3
	イ	S=4π×62＝144πcm2		イ	S=4π×32＝36πcm2
３	ア	V=π×93÷2＝486πcm3	４	ア	(半径5cmの球になるから) V＝π×53＝(500/3)πcm3
	イ	S=4π×92÷2＋92π＝243πcm2 　(注　底面積を加えること)		イ	S=4π×52＝100πcm2

［トップに戻る］ ［前ペ−ジに戻る］