|
こたえ 〜 1年5章の正答 〜 |
|
こたえ 〜 1年5章の正答 〜 |
(1) 移動
| 1 | △ADC 対称 | 2 | △ADC 回転 | 3 | △DCE 平行 | 4 | △DCB 回転 |
| 5 | △EDC 回転 | 6 | △ADC 対称 | 7 | △DEF 平行 | 8 | △DEC 回転 |
| 9 | △DEC 対称 | 10 | △DEF 回転 | ||||
(2) 平行移動
| 1 | ア | 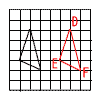 |
2 | ア | AB=DE , AB//DE BC=EF , BC//EF CA=FD , CA//FD |
| イ | 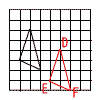 |
||||
| ウ | 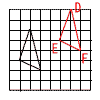 |
イ | AD=BE=CF AD//BE//CF |
(3) 回転移動
| 1 | ア | 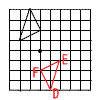 |
2 | ア | AB=DE BC=EF CA=FD |
| イ | 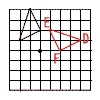 |
イ | OA=OD OB=OE OC=OF ∠AOD=∠BOE=∠COF |
||
| ウ | 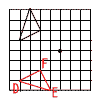 |
(4) 対称移動
| 1 | ア | 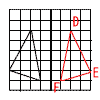 |
2 | ア | AB=DE BC=EF CA=FD |
| イ | 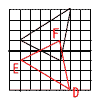 |
イ | AP=DP BQ=EQ CR=FR AD⊥ |
||
| ウ | 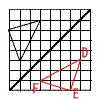 |
(5) 円とおうぎ形
| 1 | ア | 半径 ,弦 ,弧 | 2 | ア | ∠x =(180−50)÷2=75° | |
| イ | 半径 ,中心角 ,弧 | イ | ∠x =180−40×2=100° | |||
| 2 | ア | BD | ウ | 180°, 90°, ∠x =90° | ||
| イ | ∠BOD | エ | 70°, 140°, ∠x =140° | |||
| ウ |
|
|||||
(6) 円と接線
| 1 | ア | 離れている ,0 | 3 | ア | ∠x =90° |
| イ | 交わっている ,2 | イ | 90−60=30° ∠x =180−30×2=120° |
||
| ウ | 接している ,1 | ウ | 180−70×2=40° ∠x =(180−140)÷2=20° |
||
| 2 | 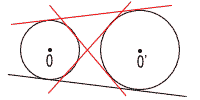 |
エ | 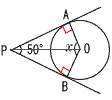 PとOを結ぶと, PとOを結ぶと,△OPAと△OPBは 直角三角形だから, ∠x =(90−25)×2 =130° |
||
(7) 直線と角
| 1 | ア | 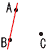 |
イ | 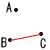 |
3 | ア | ∠x =50° |
| イ | ∠x =90° | ||||||
| ウ | 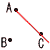 |
エ | 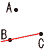 |
ウ | ∠x =180−150=30° | ||
| エ | ∠x =180−90−40=50° | ||||||
| 2 | ア | ∠d=∠e=∠h | オ | ∠x =180−(180−90−35)=125° | |||
| イ | ∠c=∠f=∠g | カ | ∠x =180−30−(180−80)=50° | ||||
| ウ | ∠j=∠k=∠l | ||||||
(8) 垂直二等分線
| 1 | 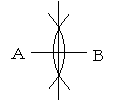 点Aと点Bから等しい 点Aと点Bから等しい半径の弧をかき,そ の交点どうしを結べ ばよい。 |
2 | 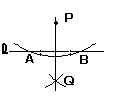 (1) 点Pから適当に (1) 点Pから適当に弧をかき,直線 の交点をA,Bとする。 (2) 点AとBから適当 に弧をかき,交点をQ とする。 (3) 点Pと点Qを結べばよい。 |
| 3 | 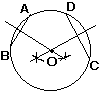 弦ABと弦CDの垂 弦ABと弦CDの垂直二等分線をひき, その交点に中心O をとればよい。 |
4 | 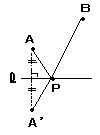 (1) 直線 (1) 直線点Aと対称な点A’を とる。 (2) 点A’と点Bを結 んで,直線 点に点Pをとる。 |
(9) 角の二等分線
| 1 | 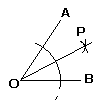 点Oから適当な弧をかき,2辺との交点から再び弧を引き,その交点をPとする。点Oと点Pを結べば,角の二等分線ができる。 点Oから適当な弧をかき,2辺との交点から再び弧を引き,その交点をPとする。点Oと点Pを結べば,角の二等分線ができる。
|
2 | 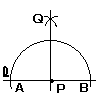 点Pから適当に弧をかき,直線 点Pから適当に弧をかき,直線 |
| 3 | ∠POC=∠AOC÷2 ∠QOC=∠BOC÷2 ∠POQ=∠POC+∠QOC =(∠AOC+∠BOC)÷2 =180÷2=90° |
4 | 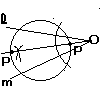 (1) 直線 (1) 直線(2) ∠Oの二等分線をひき,その交点に点Pをとる。 (点Pは2つ存在する) |
(10) いろいろな作図
| 1 | 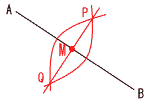 |
4 | 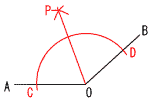 |
| 2 | 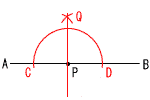 |
5 | 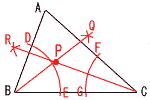 |
| 3 | 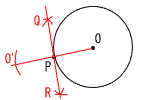 |
6 | 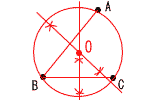 |