回答

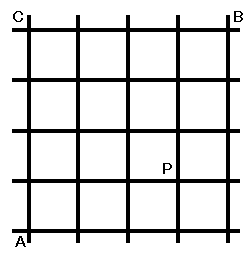
問１． 点Ａから点Ｐまでの行き方は、上に（ｎ−ｋ）回、横にｋ回進めばいいので、ｎ！/(ｎ−ｋ)！ｋ！＝_nＣ_k、
　　　　点Ｐから点Ｂまでの行き方は、上にｋ回、横に（ｎ−ｋ）回進めばいいので、ｎ！/ｋ！(ｎ−ｋ)！＝_nＣ_(n-k)、
　　　　より、_nＣ_k×_nＣ_(n-k)＝_nＣ_k×_nＣ_k＝(_nＣ_k)²通り。

問２．点Ａから点Ｂに行く時に、点Ｐを確実に通るので求める答えは、横にｎ回、縦にｎ回進む行き方と等しいので、
　　　　Σ(_nＣ_k)²(k=0,1,・・・n)＝_2nＣ_n

問３．左に進む回数と右に進む回数が同じ、かつ、上に進む回数と下に進む回数が同じでなければならない。
　　　２ｎ回のうち、ｋ回が左に、ｋ回が右に、ｍ回が上に、ｍ回が下に進むとすると、

　　　　２ｋ＋２ｍ＝２ｎ⇔ｋ＋ｍ＝ｎ

よって、求める確率は、

　　　　Σ Σ（１／４）²ⁿ×_nＣ_m×_nＣ_(n-m)×_nＣ_k×_nＣ_(n-k)(k=0,1,・・・n)(m=0,1,・・・n)

　　　　＝Σ（１／４）²ⁿ×Σ(_nＣ_m)²(m=0,1,・・・n)×Σ(_nＣ_k)²(k=0,1,・・・n)

　　　　＝（１／４）²ⁿ×(_2nＣ_n)²（２より）

補足説明

問１と問２はそれほど難しくないのですが、問３の計算が少しややこしいと思う。ｎ＝１，２あたりで試しにやってみると法則が分かりやすいと思う。